LeetCode-142.环形链表II

题目详解

相关链接

• 代码随想录

思路

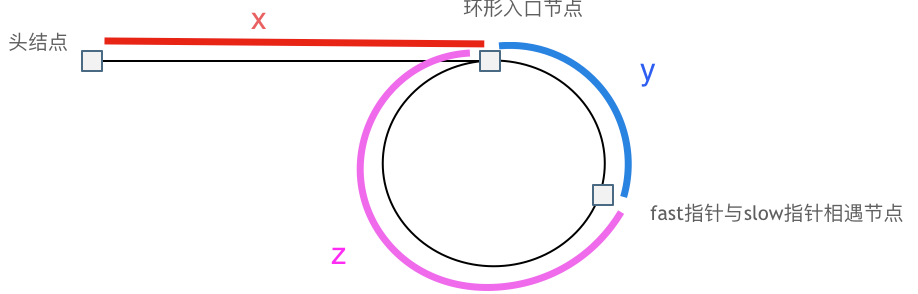
• 快慢指针。同起点，慢指针每次走一步，快指针每次走2步。如果链表有环 经数学分析可知：
  1. 两个指针一定会在环内某一点相遇
     1. 为什么在环内一定会相遇？因为快指针与慢指针的相对速度差了一步，即快指针以一步的相对速度去追慢指针，一定能追到！
     2. 相遇位置不确定，不一定是入环点
  2. 相遇时快指针走的路程是慢指针的2倍
  3. 快指针比慢指针在环内多跑了几圈，路程设为m（即m是环长的整数倍）
  4. 综上分析可知：快指针走的总路程是2m，慢指针走的总路程是m
  5. 现在只需要分析慢指针：
     1. 慢指针的轨迹可以分为两部分：
        1. 慢指针在入环前走了一段路程，设为x
        2. 入环后走了一段路程后与快指针相遇，设为y
     2. 得到x + y = m
     3. 回头看看我们的目标是找到入环点，一起分析可发现：
        1. 两个指针相遇时，慢指针在环内走的路程是y，此时距离入环点的路程是未知的
        2. 但是如果再继续走一段路程x时，则慢指针在环内的总路程达到x + y = m，而m是环长的整数倍，也就是说慢指针跑了整数圈又回到了入环点
        3. 我们不知道x、y的实际长度，但是时机我们是有办法捕获到的：
           1. 已知x就是起点与入环点的路程，而慢指针在相遇点跑了路程x也到达入环点
           2. 所以解决办法就是慢指针在相遇点开始跑时，同时起点也有一个指针开始跑，同路程同速度一定会在入环点相遇

看完代码随想录之后的想法

• 解法之前学习过，思路一致
• 我的解法主要是靠推理，卡尔给出了数学证明

实现过程中遇到的困难

• 入环点、相遇点的具体位置、距离都是未知的，只能通过特殊时机来巧妙地推理

代码

TypeScript

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     val: number
 *     next: ListNode | null
 *     constructor(val?: number, next?: ListNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.next = (next===undefined ? null : next)
 *     }
 * }
 */

function detectCycle(head: ListNode | null): ListNode | null {
  if (!head) return null
  let slow = head,
    fast = head
  while (fast && fast.next) {
    slow = slow.next
    fast = fast.next.next
    if (slow === fast) {
      while (true) {
        if (slow === head) return head
        slow = slow.next
        head = head.next
      }
    }
  }
  return null
}

时间复杂度：O(n)
空间复杂度：O(1)

收获

• 活学活用指针，就像本题不需要知道入环点、相遇点的实际位置（实际上也无法得知，不同链表是不同的），但是只需要通过合理的推理能解决问题即可